============================== \section*{A.1. Architecture}
\section*{A.1.1. Notation}
In the following, we use $L$ to denote the sequence length, $d$ for the embedding dimension, ${a . . b}$ to denote the inclusive set of integers from $a$ to $b$, and $[a, b]$ an interval of real numbers. $S E(3)$ is the special Euclidean group, which we use to denote frames (Appendix A.1.6.1).
\section*{A.1.2. Overview}
ESM3 is all-to-all generative model that both conditions on and generates a variety of different tracks. As input, ESM3 is conditioned on various tracks as described in Appendix A.1.5.1, and as output, ESM3 generates predictions detailed in Appendix A.1.5.2.
The generative pipeline is as follows.
Tokenization First, raw inputs are tokenized as described in Appendix A.1.3. Structural inputs are tokenized via a VQ-VAE (Appendix A.1.7). Function keywords are tokenized by quantizing the TF-IDF transform of functional keywords with locality sensitive hashing (LSH), detailed in Appendix A.1.8.
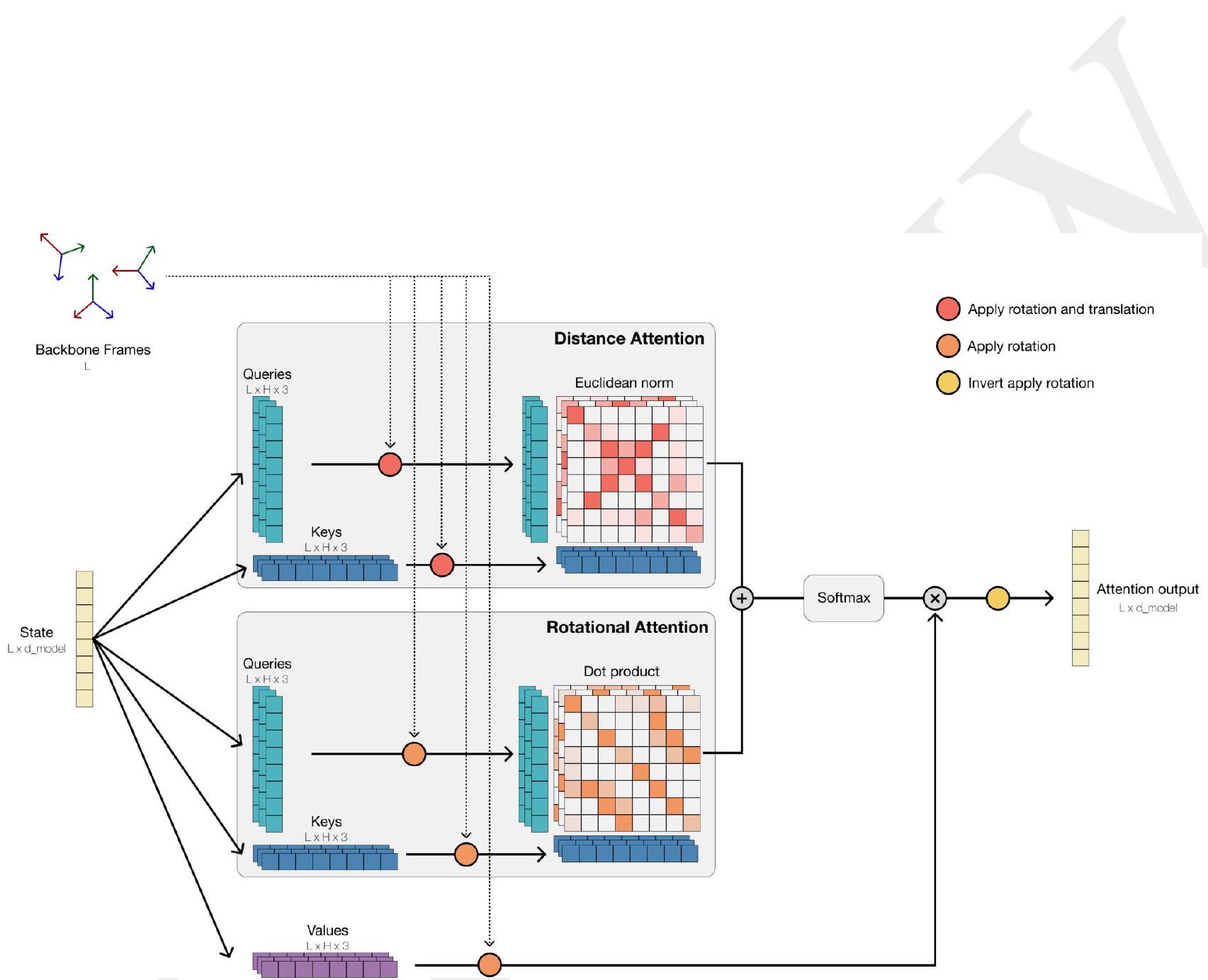
Transformer Trunk A standard Transformer $(57,58)$ architecture processes the post-tokenized inputs. Geometric Attention (Algorithm 6 and Fig. S2) directly processes structural coordinates as input. Model outputs are logits over token space, and can be sampled to obtain outputs described in Appendix A.1.5.2. The overall architecture is diagrammed in Fig. S1.
Decoder Most tracks can be naively decoded into tokens detailed in Appendix A.1.3. Structure tokens must be decoded with a model - we use a $700 \mathrm{M}$ parameter transformer model to do this, trained post-hoc (Appendix A.1.7.2). The decoder uses sequence tokens and structure tokens to directly predict coordinates, pTM, and pLDDT (59). Function tokens are decoded using a small 3-layer transformer, trained post-hoc to invert the LSH quantization procedure (Appendix A.1.8.2.1).
\section*{A.1.3. Tokenization}
t of sequences. When sequences are cropped due to length, the BOS and EOS tokens are cropped out to indicate protein fragments. In all cases, one token per track is used for each amino acid.
Sequence Protein sequences are tokenized as the 20 canon- ical amino acids, plus BOS, EOS, mask, pad, unknown. We keep four non-standard amino acids as in Lin et al. (5), B - Asparagine, U - selenocysteine, Z - glutamic acid, and O - ornithine. This totals to 29 tokens.
Structure Structure tokenization is described in Appendix A.1.7.1. ESM3 uses a codebook size of 4096 with 4 special tokens - EOS, BOS, mask, and pad.
Secondary Structure Secondary structure is taken to be the canonical 8-class tokens (60), with unknown and mask, for a total of 10 tokens. The mask token is forced to be the 0 -vector during embedding.
SASA The continuous values representing SASA are tokenized by discretization into a fixed set of 16 bins. SASA bin boundaries were chosen by computing SASA on 100 random structures and ensuring an equal number of residues belong in each bin. Unknown and mask are used for a total of 18 tokens. The mask token is forced to be the 0 -vector during embedding.
Function annotations We tokenize function annotations as bags of keywords, described in Appendix A.1.8. Keywords are quantized using LSH into 8 tokens per residue, each of which can be one of 255 tokens. There are three special tokens, empty set, no-annotation, and mask. Again, the mask token is forced to be the 0 vector during embedding.
Residue annotations InterPro annotations are tokenized as a multi-hot feature vector (1478 dimensions) over possible InterPro labels (38). Input annotations are limited to a maximum of 16 . When annotations are not present, we enforce that the 0 -vector is added.
\section*{A.1.4. ESM3 Inputs and Forward Pass}
As mentioned above, ESM3 can take several tracks, all of which are optionally disabled via masking. In the following, we concisely denote the inputs to ESM3 as
$$
The forward pass of ESM3 is then defined as
$$ \math Fi = \mathrm{Embed} \left(F{i-1} \odot M{i-1}\right) + \mathrm{MLP} \left(F{i-1} \odot M_{i-1}\right) $$
$$ \math Mi = \sigma \left(Wm F{i-1} + bm\right) $$
bf{x}{\text {inputs }}=\left{\begin{array}{l} x{\text {structure }} \in{0 . .4099}^{L}, x{\mathrm{ss} 8} \in{0 . .10}^{L} \ x{\text {sasa }} \in{0 . .18}^{L}, x{\mathrm{func}} \in{0 . .258}^{L \times 8} \ x{\mathrm{res}} \in{0,1}^{L \times 1478}, x{\mathrm{res}} \in{0,1}^{L \times 1478} \ x{\text {plddt }} \in[0,1]^{L}, x_{\text {avgplddt }} \in[0,1] \end{array}\right. $$
We now present the high level algorithm for a forward pass of ESM3:
Figure S1. The ESM3 architecture. ESM3 is a masked language model that reasons over protein sequence, structure, and function, each of which are represented as token tracks at the input and output. Tokens are embedded and summed at the input to a transformer stack. The first block (expanded on the right) contains an additional geometric attention layer for processing atomic coordinate inputs. During training, random masks are sampled and applied to each track. Masked token positions are predicted at the output.
Algorithm 1 esm3_forward
Input: $\mathbf{x}_{\text {inputs }}$
1: $z_{\text {embed }}^{(0)}=$ encode_inputs $\left(\mathbf{x}_{\text {inputs }}\right) \quad \triangleright \mathbb{R}^{L \times d}$
for $\ell \in\left\{1 . . n_{\text {layers }}\right\}$ do
$z_{\text {embed }}^{(\ell)}=$ transformer__block $\left(z_{\text {embed }}^{(\ell-1)}\right)$
end for
for track in desired output tracks do
$z_{\text {track }}=$ regression_head $\left(z_{\text {embed }}^{\left(n_{\text {layers }}\right)}\right)$
end for
return Track specific logits $z_{\text {track }} \in \mathbb{R}^{L \times c_{\text {track }}}$
In the next few sections, we detail each component.
\section*{A.1.5. Transformer}
dimension is set to approximately $\frac{8}{3} d$, rounded to the nearest multiple of 256 for training efficiency. No biases are used in linear layers or layer norms, as suggested by PaLM (63). We have observed through the literature and in internal experiments that these architecture changes improve the stability and performance of models.
A core architectural modification we make is the insertion of the Geometric Attention sub-layer in the first block of the network only (Appendix A.1.5, line 3).
Algorithm 2 transformer_block
Input: $x \in \mathbb{R}^{L \times d}, T \in S E(3)^{L}$
1: $s=\sqrt{\frac{36}{n_{\text {layers }}}}$
2: $x=x+s \cdot$ MultiHeadSelfAttention $(x) \quad \triangleright \mathbb{R}^{L \times d}$
3: $x=x+s$. geometric_mha $(x, T) \quad \triangleright \mathbb{R}^{L \times d}$
4: $x=x+s \cdot \operatorname{SwiGLUMLP}(x) \quad \triangleright \mathbb{R}^{L \times d}$
ESM3-small (1.4B) is a 48-layer network, while ESM3medium (7B) has 96 layers, and ESM3-large (98B) has 216 layers. We experimented with different width-to-depth ratios and observed higher returns for depth than width. Prior work also demonstrates that modalities like ours benefit more from deeper networks $(64,65)$. Detailed network specifications can be found in Table S1.
\section*{A.1.5.1. EMBEDDING}
There are 7 unique input tracks to ESM3: (a) sequence (amino acid tokens), (b) structure coordinates, (c) struc- ture tokens, (d) 8-class secondary structure labels (SS8), (e) quantized solvent-accessible surface area (SASA) values, (f) function keyword tokens and (g) residue (InterPro) annotation binary features.
There are two additional tracks used during pre-training only: (h) per-residue confidence (pLDDT) and (i) averaged confidence (pLDDT). At inference time, these values are fixed, and these tracks are equivalent to adding a constant vector $z_{\text {plddt }}$.
Structure coordinates are parsed through the Geometric Attention and are not embedded.
r keyword-based function tokens, each of the eight integers per residue is converted to a "sub-embedding" (Appendix A.1.5.1 line 5), then concatenated to form the perresidue embedding (Appendix A.1.5.1 line 6). For InterPro residue annotations, the inputs are multi-hot. To create an embedding vector, we sum the embeddings for each of the "on" features (equivalent to the matrix-multiply on Appendix A.1.5.1 line 7).
The largest model, 98B has an additional taxonomy track detailed in Appendix A.1.9.2, only enabled in the final $30 \mathrm{~K}$ steps of pre-training.
The embeddings are all summed as input to the first layer in the network architecture.
Algorithm 3 encode_inputs
Input: $\mathrm{x}_{\text {inputs }}=$
$\left\{x_{\text {seq }}, x_{\text {structure }}, x_{\text {ss } 8}, x_{\text {sasa }}, x_{\text {func }}, x_{\text {res }}, x_{\text {plddt }}, x_{\text {avgplddt }}\right\}$
$z_{\text {seq }}=\operatorname{embed}\left(x_{\text {seq }}\right) \quad \triangleright \mathbb{R}^{L \times d}$
$z_{\text {structure }}=\operatorname{embed}\left(x_{\text {structure }}\right) \quad \triangleright \mathbb{R}^{L \times d}$
$z_{\mathrm{ss} 8}=\operatorname{embed}\left(x_{\mathrm{ss} 8}\right) \quad \triangleright \mathbb{R}^{L \times d}$
$z_{\text {sasa }}=\operatorname{embed}\left(x_{\text {sasa }}\right) \quad \triangleright \mathbb{R}^{L \times d}$
$h_{\text {func }, i}=\operatorname{embed}\left(\left[x_{\text {func }}\right]_{:, i}\right) \quad \triangleright \mathbb{R}^{L \times \frac{d}{8}}$
$z_{\text {func }}=\left[h_{\text {func }, 1}\left|h_{\text {func }, 2}\right| \ldots \mid h_{\text {func }, 8}\right] \quad \Delta \mathbb{R}^{L \times d}$
$z_{\text {res }}=x_{\mathrm{res}} W_{\text {res }} \quad \triangleright \mathbb{R}^{L \times d}$
$z_{\text {plddt }}=$ plddt_embed $\left(x_{\text {plddt }}, x_{\text {avgplddt }}\right) \quad \triangleright \mathbb{R}^{L \times d}$
return $z_{\text {seq }}+z_{\text {plddt }}
------------------------------
- The inputs are encoded using the encode_inputs algorithm.
- The inputs include x_seq, x_structure, x_ss8, x_sasa, x_func, x_res, and x_plddt.
- The inputs are encoded using the embed function.
- The encoded inputs are concatenated to form the final embedding vector.
- The largest model, 98B, has an additional taxonomy track.
- The embeddings are summed as input to the first layer in the network architecture.
==============================
+z_{\text {structure }}+z_{\text {ss } 8}+z_{\text {sasa }}+z_{\text {func }}+z_{\text {res }}$
\section*{A.1.5.2. LOGITS}
We use a regressionhead to take in $d$ dimensional last layer hidden features and produce $c{\text {track }}$-dimensional logits for each of the tracks, where $c{\text {track }}$ corresponds to the size of the vocabulary per track. Note that for the keyword function tokens, we produce $c{\text {func }} \times 8$ logits, and softmax over each of the 8 independently when calculating the loss.
\begin{tabular}{lllllllllll} \hline Params & $n{\text {layers }}$ & $d{\text {model }}$ & $d_{\text {head }}$ & \begin{tabular}{l} Context \ length \end{tabular} & \begin{tabular}{l} Learning Warmup \ rate \end{tabular} & \begin{tabular}{l} Batch \ steps \ size in \ tokens \end{tabular} & \begin{tabular}{l} Num \ steps \end{tabular} & \begin{tabular}{l} Total \ tokens \end{tabular} & FLOPs \ \hline 1.4B & & & & & & & & & \ 1.4B & 48 & 1536 & 64 & 2048 & $4.0 \mathrm{e}-4$ & $5 \mathrm{~K}$ & $1,572,864$ & $50 \mathrm{~K}$ & $\sim 80 \mathrm{~B}$ & $6.72 \times 10^{20}$ \ 7.7B & 96 & 2560 & 64 & 2048 & $4.0 \mathrm{e}-4$ & $5 \mathrm{~K}$ & $1,572,864$ & $200 \mathrm{~K}$ & $\sim 320 \mathrm{~B}$ & $2.7 \times 10^{21}$ \ 98.5B & 216 & 6144 & 128 & 2048 & $2.5 \mathrm{e}-4$ & $5 \mathrm{~K}$ & $3,932,160$ & $140 \mathrm{~K}$ & $\sim 550 \mathrm{~B}$ & $2.47 \times 10^{22}$ \ \hline \end{tabular}
Table S1. Parameter details for different model configurations.
Algorithm 4 regression_head
Input: $x \in \mathbb{R}^{\cdots \times d}$
1: $z=\operatorname{proj}_{\text {in }}(x)$
2: $z=\operatorname{GeLU}(z)$
3: $z=\operatorname{LayerNorm}(z)$
4: $z=\operatorname{proj}_{\text {out }}(z)$
return $z$
due (InterPro) annotation binary features.
Except for the multi-hot residue annotations, all other tracks are predicted as a categorical distribution over possible tokens.
\section*{A.1.6. Geometric Attention}
As mentioned in Appendix A.1.5.1, ESM3 processes structural information in two independent ways:
Geometric Attention Described in Algorithm 6, this leverages fine-grained 3D information via conditioning on exact coordinates. We find that conditioning on coordinates is critical to good inverse folding performance. Coordinates are only used as model inputs.
Structure Tokens Described in Appendix A.1.7, structure tokens enable faster learning due to rich local neighborhood semantics being compressed into tokens. Structure tokens are generally used as model outputs.
Geometric attention enables high-throughput encoding of protein structures. Protein backbone structure can be represented by the relative distance and orientation of frames defined by each residue's backbone coordinates. Reasoning over the relative orientation of frames is important to capture the local backbone geometry when only partial structure is provided. Geometric attention is an $S E(3)$ invariant allto-all attention mechanism which reasons over the relative distances and orientations of all defined frames in the input (Fig. S2). Because this attention operation can be realized using the same computational primitives as attention, it is readily scalable.
We first provide an overview of frames, and then describe how geometric attention uses them:
\section*{A.1.6.1. FRAMES}
Frames are representations that encapsulate the 3D positional and rotational information of residue backbones and sidechains in a protein structure. We use a formulation similar to Ingraham et al. (66). Each frame $T \in S E(3)$ consists of a rotation matrix $\mathbf{R} \in S O(3)$ and a translation vector $\mathbf{t} \in \mathbb{R}^{3}$
Definition: A frame $T_{i}$ for residue $i$ is defined as:
$$
n{array}{cc} \mathbf{R}{i} & \mathbf{t}{i} \ \mathbf{0}_{1 \times 3} & 1 \end{array}\right] \in S E(3) $$
where $\mathbf{R}{i} \in S O(3)$ and $\mathbf{t}{i} \in \mathbb{R}^{3}$.
Rotation Matrix: The rotation matrix $\mathbf{R}{i}$ for residue $i$ is composed of three 3-dimensional vectors $\left[\hat{x}, \hat{e}{1}, \hat{e}_{2}\right]$ :
This matrix rotates vectors to a local coordinate system where the $N-C_{\alpha}-C$ plane for the corresponding residue spans the $x y$ plane.
Translation Vector: The translation vector $\mathbf{t}{i}$ specifies the position of the residue's $C{\alpha}$.
Transformation: To transform a point $\mathbf{p} \in \mathbb{R}^{3}$ from the local frame of residue $i$ to the global coordinate system, the following equation is used:
$$ \mathbf{p}{\text {global }}=T{i}(\mathbf{p})=\mathbf{R}{i} \mathbf{p}+\mathbf{t}{i} $$
Inverse Transformation: To transform a point $\mathbf{p}_{\text {global }} \in$ $\mathbb{R}^{3}$ from the global coordinate system back to the local frame of residue $i$, the following equation is used:
$$ \mathbf{p}=T{i}^{-1}\left(\mathbf{p}{\text {global }}\right)=\mathbf{R}{i}^{-1}\left(\mathbf{p}{\text {global }}-\mathbf{t}_{i}\right) $$

put comparable to the standard attention operation in transformers.
To create frames, all we require is a translation vector $\vec{t}$, and two vectors $\vec{x}$ and $\vec{y}$ defining the local $x y$ plane after conversion to global coordinates, from which the frame $T$ can be calculated with the standard Gram-Schmidt algorithm:
Algorithm 5 gram_schmidt
Input: $\vec{t} \in \mathbb{R}^{L \times 3}, \vec{x} \in \mathbb{R}^{L \times 3}, \vec{y} \in \mathbb{R}^{L \times 3}$
$: \hat{x}=\frac{\vec{x}}{\|\vec{x}\|}$
$\vec{e}_{1}=\vec{y}-(\hat{x} \cdot \vec{y}) \hat{x}$
$\hat{e}_{1}=\frac{\vec{e}_{1}}{\left\|\vec{e}_{1}\right\|}$
$\hat{e}_{2}=\hat{x} \times \hat{e}_{1}$
$R=\left[\hat{x}, \hat{e}_{1}, \hat{e}_{2}\right] \quad \triangleright S O(3)^{L}$
$T=\left[\begin{array}{cc}R & \vec{t} \\ 0_{1} \times 3 & 1\end{array}\right] \quad \triangleright S E(3)^{L}$
return $T$
We construct frames such that the $C_{\alpha}$ is at the origin of the frame $(\vec{t}), C$ on the negative x-axis $(-\vec{x})$, and $N$ is on the $x y$-plane.
\section*{A.1.6.2. GEOMETRIC SELF-ATTENTION}
Algorithm 6 details the Geometric Self-Attention layer. It can be efficiently implemented using similar ideas as FlashAttention (33). It is used twice in our system: in the VQ-VAE encoder for structure tokens (Appendix A.1.7.1), and in the first layer of ESM3.
Unlike regular self-attention, which only operates on perresidue embeddings, Geometric Attention incorporates the per-residue frames $T$ to integrate geometric information in a rotation and translation invariant way. The process of forming the attention matrix $A$ is as follows:
, keys and values are initially assumed to be in the local frame of their corresponding residue.
(a) Convert to Global Rotational Frame: We convert each of the vectors in $Q{r}, K{r}, V$ from their local frame (where the $x y$ plane is the $N-C{\alpha}-C$ plane for each residue) to a global rotational frame (where the $x y$ plane is aligned for all residues) by applying $\mathbf{R}{i}$ (Algorithm 6, lines 3, 4).
(b) Convert to Global Distance Frame: We convert each of the vectors in $Q{d}, K{d}$ from their local frame to a global frame by applying $T_{i}$ (Algorithm 6 , lines 5, 6).
Directional Attention: The pairwise, per-head $h$ rotational similarity $R$ between keys $i$ and queries $j$ is calculated using the dot product $[R]{i, j, h}=\frac{1}{\sqrt{3}}\left[q{r}\right]{i, h,:}$. $\left[k{r}\right]_{j, h,:}$ This is equivalent to the cosine distance between projected points.
Distance Attention: The pairwise, per-head $h$ distance similarity $D$ between keys $i$ and queries $j$ is computed using the $L{2}$ norm of the difference $[D]{i, j, h}=$ $\frac{1}{\sqrt{3}}\left|\left[q{r}\right]{i, h,:}-\left[k{r}\right]{j, h,:}\right|_{2}$.
Scale Factor: $R$ and $D$ are scaled per-head with learned scalars $\left[\bar{w}{r}\right]{h}$ and $\left[\bar{w}{d}\right]{h}$, respectively, where $\bar{w}{r}, \bar{w}{d} \in \mathbb{R}^{h}$. We use the softplus function to transform weights into $[0, \infty)^{h}$. This scaling allows certain heads to specialize in attending via distance or directional attention.
Algorithm 6 geometric_mha
Input: $X \in \mathbb{R}^{L \times d}, T \in S E(3)^{L}$
$Q_{r}, K_{r}, Q_{d}, K_{d}, V=\operatorname{Linear}(X) \quad \triangleright\left(\mathbb{R}^{L \times h \times 3}\right)_{\times 5}$
$\left(\mathbf{R}_{i}, \mathbf{t}_{i}\right)=T_{i} \quad \triangleright\left(S O(3)^{L}, \mathbb{R}^{L \times 3}\right)$
$\left[Q_{r}\right]_{i, h,:}=\mathbf{R}_{i}\left(\left[Q_{r}\right]_{i, h,:}\right) \
------------------------------
- $Q_{r}$ is a matrix in the local frame of each residue.
- $K_{r}$ is a matrix in the local frame of each residue.
- $V$ is a matrix in the local frame of each residue.
- $Q_{d}$ is a matrix in the local frame of each residue.
- $K_{d}$ is a matrix in the local frame of each residue.
- $T_{i}$ is a matrix that converts vectors from the local frame to the global frame for each residue.
- $R$ is a matrix that calculates the rotational similarity between keys and queries.
- $D$ is a matrix that calculates the distance similarity between keys and queries.
- $\bar{w}_{r}$ is a vector of learned scalars for the rotational attention heads.
- $\bar{w}_{d}$ is a vector of learned scalars for the distance attention heads.
- $\mathbf{R}_{i}$ is a matrix that converts vectors from the local frame to the global rotational frame for each residue.
- $\mathbf{t}_{i}$ is a matrix that converts vectors from the local frame to the global distance frame for each residue.
User:
==============================
quad \triangleright \mathbb{R}^{L \times h \times 3}$
$\left[K_{r}\right]_{i, h,:}=\mathbf{R}_{i}\left(\left[K_{r}\right]_{i, h,:}\right)$
$\triangleright \mathbb{R}^{L \times h \times 3}$
$\left[Q_{d}\right]_{i, h,:}=T_{i}\left(\left[Q_{d}\right]_{i, h,:}\right) \quad \triangleright \mathbb{R}^{L \times h \times 3}$
$\left[K_{d}\right]_{i, h,:}=T_{i}\left(\left[K_{d}\right]_{i, h,:}\right) \quad \triangleright \mathbb{R}^{L \times h \times 3}$
$7:[R]_{i, j, h}=\frac{1}{\sqrt{3}}\left[q_{r}\right]_{i, h,:} \cdot\left[k_{r}\right]_{j, h,:} \quad \triangleright \mathbb{R}^{L \times L \times h}$
8: $[D]_{i, j, h}=\frac{1}{\sqrt{3}}\left\|\left[q_{r}\right]_{i, h,:}-\left[k_{r}\right]_{j, h,:}\right\|_{2} \quad \triangleright \mathbb{R}^{L \times L \times h}$
9: $A=\operatorname{softplus}\left(\bar{w}_{r}\right) R-\operatorname{softplus}\left(\bar{w}_{d}\right) D \quad \triangleright \mathbb{R}^{L \times L \times h}$
$A=\operatorname{softmax}_{j}(A)$
$[V]_{i, h,:}=\mathbf{R}_{i}\left([V]_{i, h,:}\right)$
$O=A \cdot V \quad \triangleright \mathbb{R}^{L \times h \times 3}$
$[O]_{i, h,:}=\mathbf{R}_{i}^{-1}\left([O]_{i, h,:}\right)$
$X=X+\operatorname{Linear}(O)$
$\triangle \mathbb{R}^{L \times d}$
\section*{A.1.7. Structure Tokenizer}
Each residue is associated with one of 4,096 structure tokens ( +4 special tokens), designed to provide a rich, learned representation of its local neighborhood. The tokens are generated with a VQ-VAE encoder, with a corresponding decoder to enable decoding of generated tokens back to $3 \mathrm{D}$ coordinates.
\section*{A.1.7.1. ENCODER}
The VQ-VAE encoder $f{\text {enc }}$ consists of two geometric attention blocks (Transformer blocks, but self-attention replaced with geometricmha) with an embedding width of 1024 and 128 geometric heads per geometric attention layer.
The VQ-VAE encoder reasons over the backbone frames
structure. Relative sequence positions are encoded through a learned positional embedding. Sequence positions are determined relative to the query residue (i.e., if the query residue has residue index 56 , then the residue in index 58 has a +2 sequence position). Relative sequence positions are clamped to $+/-32$ before encoding, meaning long-range contacts share sequence positional embeddings. Relative sequence positional embeddings define the initial encoder state $N$, and has shape $L \times 16 \times d$ (Algorithm 7, line 4). Note that this means the input to the VQ-VAE encoder is purely structural: no sequence (amino acid), function or other information is used here. Furthermore, each neighborhood is processed completely independently; for each residue, the encoder only uses the information of its 16 nearest neighbors.
Geometric attention blocks operate similar to Transformer blocks in that they transform a state according to an attention operation ( geometricmha ) and feedforward network (SwiGLU MLP). As such, the output has the same shape as the input. In this case, this means that the encoder outputs 16 latents per residue. However, we want to learn a single token, i.e., a single latent per residue, hence we take the embedding corresponding to the query residue position $N{:, 0,:}$.
The process of generating structure tokens (Algorithm 7) from the full 3D coordinates of the protein then is as follows:
Local Neighborhood: For each residue, obtain the indices $N{\text {idx }} \in{0 . . L-1}^{L \times 16}$ of the 16 nearest residues (as measured by $C{\alpha}$ distance). The first of the 16 neighbors is always the residue itself. We also obtain the frames for each residue in a local neighborhood with $T_{\text {knn }}$.
Embed Neighbors: Embed the relative distance in sequence space for each neighbor, $\Delta i=\operatorname{clamp}\left(N_{\mathrm{idx}}-\right.$ $i,-32,32$ ) to form $N \in \mathbb{R}^{L \times 16 \times d}$
through a shallow encoder $f{\text {enc }}$ consisting of 2 Transformer blocks, with regular multihead self-attention swapped with geometricmha. The attention is unmasked, all-to-all over the entire neighborhood.
Input: $x_{C_{\alpha}} \in \mathbb{R}^{L \times 3}, T \in S E(3)^{L}$
1: $N_{\mathrm{idx}}=\operatorname{knn}\left(x_{C_{\alpha}}\right) \quad \triangleright\{0 . . L-1\}^{L \times 16}$
$: T_{\mathrm{knn}}=T\left[N_{\mathrm{idx}}\right] \quad \triangleright S E(3)^{L \times 16}$
$\Delta i=\operatorname{clamp}\left(N_{\mathrm{idx}}-i,-32,32\right)$
$N=\operatorname{embed}(\Delta i)$
$\Delta \mathbb{R}^{L \times 16 \times d}$
5: $N=f_{\text {enc }}\left(N, T_{\mathrm{knn}}\right)$
$\triangle \mathbb{R}^{L \times 16 \times d}$
6: $z=\operatorname{Linear}\left(N_{:, 0,:}\right) \quad \triangleright \mathbb{R}^{L \times d^{\prime}}$
7: $z=$ quantize $(z) \quad \triangleright\{0 . .4095\}^{L \times 16}$
\section*{A.1.7.1.1. Codebook Learning}
quantize transforms the $L$ latents into $L$ discrete tokens. Since the VQ-VAE was initially proposed (67), numerous approaches and tricks have been developed to address issues with poor codebook utilization and unstable training. We chose to learn the codebook as an exponential moving average of encoder outputs (67-69). To improve codebook utilization, unused codes are re-initialized to encoder outputs.
\section*{A.1.7.1.2. Parallel Encoding}
\times 16 \times d$.
\section*{A.1.7.2. DECODER}
While the encoder independently processes all local structures in parallel, the decoder $f_{\text {dec }}$ attends over the entire set of $L$ tokens to reconstruct the full structure. It is composed using a stack of bidirectional Transformer blocks with regular self-attention.
As discussed in Appendix A.1.7.3, the VQ-VAE is trained in two stages. In the first stage, a smaller decoder trunk consisting of 8 Transformer blocks with width 1024, rotary positional embeddings, and MLPs is trained to only predict backbone coordinates. In the second stage, the decoder weights are re-initialized and the network size is expanded to 30 layers, each with an embedding dimension of 1280 ( $\sim 600 \mathrm{M}$ parameters) to predict all atom coordinates.
The exact steps to convert structure tokens back to 3D allatom coordinates using the decoder is provided in Algorithm 8 and detailed as follows,
Transformer: We embed the structure tokens and pass them through a stack of Transformer blocks $f_{d e c}$ (regular self-attention + MLP sublayers, no geometric attention).
Projection Head: We use a projection head to regress 3 3-D vectors per residue: a translation vector $\vec{t}$, and 2 vectors $-\vec{x}$ and $\vec{y}$ that define the $N-C_{\alpha}-C$ plane per residue after it has been rotated into position. This head also predicts the unnormalized sine and cosine components of up to 7 sidechain torsion angles.
Calculate $T$ : We use gram_schmidt to convert $\vec{t}$, $\vec{x}$, and $\vec{y}$ into frames $T \in S E(3)^{L}$.
Calculate $T{\text {local }}$ : We normalize the sine and cosine components and convert them to frames $T{\text {local }} \in$ $S E(3)^{L \times 7}$ corresponding to rotations around the previous element on the sidechain.
ponding to the transformations needed for each heavy atom per residue in atom14 representation.
Algorithm 8 structure_decode
Input: $z \in\{0 . .4099\}^{L \times 16}$
1: $z=\operatorname{embed}(z)$
$\triangle \mathbb{R}^{L \times d}$
2: $z=f_{d e c}(z)$
$\triangleright \mathbb{R}^{L \times d}$
3: $\vec{t}, \vec{x}, \vec{y}, \sin \theta, \overline{\cos \theta}=\operatorname{proj}(z) \quad \triangleright\left(\mathbb{R}^{L \times 3}\right)_{\times 3},\left(\mathbb{R}^{L \times 7}\right)_{\times 2}$
4: $T=$ gram_schmidt $(\vec{t},-\vec{x}, \vec{y}) \quad \triangle S E(3)^{L}$
5: $\sin \theta=\frac{\overline{\sin \theta}}{\sqrt{\sin ^{2}+\overline{\cos \theta}}} \quad \triangleright[-1,1]^{L \times 7}$

7: $T_{\text {local }}=$ rot_frames $(\sin \theta, \cos \theta) \quad \triangleright S E(3)^{L \times 7}$
8: $T_{\text {global }}=$ compose $\left(T_{\text {local }}, T\right) \quad \triangleright S E(3)^{L \times 14}$
9: $\vec{X}=T_{\text {global }}\left(\overrightarrow{X_{r e f}}\right) \quad \triangleright \mathbb{R}^{L \times 14 \times 3}$
\section*{A.1.7.3. TRAINING}
When using a VQ-VAE to learn discrete representations which maximize reconstruction quality, it is common to train in the autoencoder in two stages (70). In the first stage, the encoder and codebook is learned with a relatively small and efficient decoder. In the second stage, the encoder and codebook are frozen and a larger or otherwise more computationally expensive decoder is trained to maximize reconstruction quality. We follow this two-stage training approach for the structure tokenizer.
on*{A.1.7.3.1. Stage 1.}
The VQ-VAE is trained for $90 \mathrm{k}$ steps on a dataset of single chain proteins from the PDB, AFDB, and ESMAtlas. We use the AdamW optimizer (Loshchilov et al. 2017) with learning rate annealed from $4 \mathrm{e}-4$ according to a cosine decay schedule. Proteins are cropped to a maximum sequence length of 512. Five losses are used to supervise this stage of training. The geometric distance and geometric direction losses are responsible for supervising reconstruction of high quality backbone structures.
Additionally, a distogram and binned direction classification loss are used to bootstrap structure prediction but are ultimately immaterial to reconstruction. We have found that these structure prediction losses formulated as classification tasks improve convergence early in training. To produce these pairwise logits, we use a pairwiseprojhead, that takes $x \in \mathbb{R}^{L \times d}$ and returns logits $z \in \mathbb{R}^{L \times L \times d^{\prime}}$. It works as follows:
Algorithm 9 pairwise_proj_head
Input: $x \in \mathbb{R}^{L \times d}$
$q, k=\operatorname{proj}(x), \operatorname{proj}(x)$
$: \operatorname{prod}_{i, j,:} \operatorname{diff}_{i, j,:}=q_{j,:} \odot k_{i,:}, q_{j,:}-k_{i,:}$
$z=$ regression_head $([$ prod $\mid$ diff $]) \triangleright \mathbb{R}^{L \times L \times d^{\prime}}$
return $z$
Finally, an inverse folding token prediction loss (i.e., a crossentropy loss between predicted sequence and ground truth sequence) is an auxiliary loss used to encourage the learned representations to contain information pertinent to sequencerelated tasks.
The five losses are covered in detailed as follows:
error to $(5 \AA)^{2}$, and take the mean.
Algorithm 10 backbone_distance_loss
Input: $\hat{X} \in \mathbb{R}^{L \times 3 \times 3}, X \in \mathbb{R}^{L \times 3 \times 3}$
: $\hat{Z}, Z=\operatorname{flatten}(\hat{X})$, flatten $(X) \quad \triangleright \mathbb{R}^{3 L \times 3}, \mathbb{R}^{3 L \times 3}$
$\left[D_{\text {pred }}\right]_{i, j}=\left\|[\hat{Z}]_{i,:}-[\hat{Z}]_{j,:}\right\|_{2}^{2} \quad \triangleright \mathbb{R}^{3 L \times 3 L}$
$[D]_{i, j}=\left\|[Z]_{i,:}-[Z]_{j,:}\right\|_{2}^{2} \quad \triangleright \mathbb{R}^{3 L \times 3 L}$
$E=\left(D_{\text {pred }}-D\right)^{2}$
$E=\min (E, 25)$
$l=\operatorname{mean}_{i, j}(E)$
$\triangle \mathbb{R}$
return $l$
(b) $C_{\alpha} \rightarrow C$
(c) $C \rightarrow N_{\text {next }}$
(d) $\mathbf{n}{C{\alpha}}=-\left(N \rightarrow C{\alpha}\right) \times\left(C{\alpha} \rightarrow C\right)$
(e) $\mathbf{n}{N}=\left(C{\text {prev }} \rightarrow N\right) \times\left(N \rightarrow C_{\alpha}\right)$
(f) $\mathbf{n}{C}=\left(C{\alpha} \rightarrow C\right) \times\left(C \rightarrow N_{\text {next }}\right)$
Compute the pairwise dot product, forming $D{\text {pred }}, D \in$ $\mathbb{R}^{6 L \times 6 L}$. Compute $\left(D{\text {pred }}-D\right)^{2}$, clamp the maximum error to 20 , and take the mean.
In algorithm form (with compute_vectors computing the six vectors described above):
Algorithm 11 backbone_direction_loss
Input: $\hat{X} \in \mathbb{R}^{L \times 3 \times 3}, X \in \mathbb{R}^{L \times 3 \times 3}$
$\hat{V}=$ compute_vectors $(\hat{X}) \quad \triangleright \mathbb{R}^{6 L \times 3}$
$V=$ compute_vectors $(X) \quad \triangle \mathbb{R}^{6 L \times 3}$
$\left[D_{\text {pred }}\right]_{i, j}=[\hat{V}]_{i,:} \cdot[\hat{V}]_{j,:} \quad \triangleright \mathbb{R}^{6 L \times 6 L}$
$[D]
------------------------------
_{i, j}=[V]_{i,:} \cdot[V]_{j,:} \quad \triangleright \mathbb{R}^{6 L \times 6 L}$
$E=\left(D_{\text {pred }}-D\right)^{2}$
$E=\min (E, 20)$
$l=\operatorname{mean}_{i, j}(E)$
$\triangle \mathbb{R}$
return $l$
(b) $C \rightarrow N_{\text {next }}$
(c) $\mathbf{n}{C}=\left(C{\text {prev }} \rightarrow N\right) \times\left(N \rightarrow C_{\alpha}\right)$
Compute the pairwise dot product, forming $D{\text {pred }}, D \in$ $\mathbb{R}^{3 L \times 3 L}$. Compute $\left(D{\text {pred }}-D\right)^{2}$, clamp the maximum error to 20 , and take the mean.
In algorithm form (with compute_vectors computing the three vectors described above):
Algorithm 12 sidechain_direction_loss
Input: $\hat{X} \in \mathbb{R}^{L \times 3 \times 3}, X \in \mathbb{R}^{L \times 3 \times 3}$
$\hat{V}=$ compute_vectors $(\hat{X}) \quad \triangleright \mathbb{R}^{3 L \times 3}$
$V=$ compute_vectors $(X) \quad \triangle \mathbb{R}^{3 L \times 3}$
$\left[D_{\text {pred }}\right]_{i, j}=[\hat{V}]_{i,:} \cdot[\hat{V}]_{j,:} \quad \triangleright \mathbb{R}^{3 L \times 3 L}$
$[D]_{i, j}=[V]_{i,:} \cdot[V]_{j,:} \quad \triangleright \mathbb{R}^{3 L \times 3 L}$
$E=\left(D_{\text {pred }}-D\right)^{2}$
$E=\min (E, 20)$
$l=\operatorname{mean}_{i, j}(E)$
$\triangle \mathbb{R}$
return $l$
In algorithm form:
Algorithm 13 ramachandran_plot_loss
Input: $\hat{X} \in \mathbb{R}^{L \times 3 \times 3}, X \in \mathbb{R}^{L \times 3 \times 3}$
$\hat{V}=$ compute_vectors $(\hat{X}) \quad \triangleright \mathbb{R}^{6 L \times 3}$
$V=$ compute_vectors $(X) \quad \triangle \mathbb{R}^{6 L \times 3}$
$\left[D_{\text {pred }}\right]_{i, j}=[\hat{V}]_{i,:} \cdot[\hat{V}]_{j,:} \quad \triangleright \mathbb{R}^{6 L \times 6 L}$
$[D]_{i, j}=[V]_{i,:} \cdot[V]_{j,:} \quad \triangleright \mathbb{R}^{6 L \times 6 L}$
$E=\left(D_{\text {pred }}-D\right)^{2}$
$E=\min (E, 20)$
$l=\operatorname{mean}_{i, j}(E)$
$\triangle \mathbb{R}$
return $l$
In algorithm form:
Algorithm 14 secondary_structure_loss
Input: $\hat{X} \in \mathbb{R}^{L \times 3 \times 3}, X \in \mathbb{R}^{L \times 3 \times 3}$
$\hat{V}
==============================
_{i, j}=[V]_{i,:} \cdot[V]_{j,:} \quad \triangleright \mathbb{R}^{6 L \times 6 L}$
$E=\left(D_{\text {pred }}-D\right)^{2}$
$E=\min (E, 20)$
$l=\operatorname{mean}_{i, j}(E) \quad \triangleright \mathbb{R}$
return $l$
(a) Unit vectors: Compute three vectors per residue from ground truth coordinates: $C{\alpha} \rightarrow C, C{\alpha} \rightarrow$ $N$, and $\mathbf{n}{C{\alpha}}=\left(C{\alpha} \rightarrow C\right) \times\left(C{\alpha} \rightarrow N\right)$, and normalize them to unit length.
(b) Dot Products: Compute pairwise dot products between each pair of vectors for all residues, forming $D \in[-1,1]^{L \times L \times 6}$. Bin the dot products into 16 evenly spaced bins in $[-1,1]$, forming classification labels $y \in{0 . .15}^{L \times L}$.
(c) Pairwise Logits: Pass the final layer representations of the decoder $h \in \mathbb{R}^{L \times d}$ through a pairwiseprojhead to obtain logits $z \in$ $\mathbb{R}^{L \times L \times 6 \times 16}$.
(d) Cross Entropy: Calculate cross-entropy loss using the labels $y$ from the ground truth structure and the logits $z$, and average over all $L \times L \times 6$ values.
The process of computing unit vectors from ground truth coordinates involves computing three vectors per residue from $C{\alpha} \rightarrow C, C{\alpha} \rightarrow N$, and $\mathbf{n}{C{\alpha}}=\left(C{\alpha} \rightarrow C\right) \times\left(C{\alpha} \rightarrow N\right)$.
The process of computing pairwise dot products between each pair of vectors for all residues involves forming a matrix $D \in[-1,1]^{L \times L \times 6}$ and binning the dot products into 16 evenly spaced bins in $[-1,1]$, forming classification labels $y \in{0 . .15}^{L \times L}$.
The process of computing pairwise logits involves passing the final layer representations of the decoder $h \in \mathbb{R}^{L \times d}$ through a pairwiseprojhead to obtain logits $z \in$ $\mathbb{R}^{L \times L \times 6 \times 16}$.
The process of calculating the Distogram Loss involves calculating $C{\beta}$ given the ground truth $N, C{\alpha}$, and $C$ coordinates, and computing a cross-entropy between these targets and pairwise logits.
} \rightarrow C\right)$.
ii. Define the following scalars:
$$ \begin{aligned} a & =-0.58273431 \ b & =0.56802827 \ c & =-0.54067466 \end{aligned} $$
iii. Compute the location of $C_{\beta}$ using the formula:
$C{\beta}=a \mathbf{n}+b\left(N \rightarrow C{\alpha}\right)+c\left(C{\alpha} \rightarrow C\right)+C{\alpha}$
(b) Pairwise $C{\beta}$ distances: Compute an $L \times L$ pairwise distance matrix of the $C{\beta}$, and bin them into one of 64 bins, with lower bounds $\left[0,2.3125^{2},(2.3125+0.3075)^{2}, \ldots, 21.6875^{2}\right]$, forming the labels $y \in{0 . .63}^{L \times L}$.
(c) Pairwise logits: Pass the final layer representations of the decoder $h \in \mathbb{R}^{L \times d}$ through a pairwiseprojhead to obtain the logits $z \in \mathbb{R}^{L \times L \times 64}$.
(d) Cross Entropy: Calculate the cross-entropy using the labels $y$ computed from the ground truth structure and the logits $z$, then average over all $L \times L$ values.
\section*{A.1.7.3.2. Stage 2.}
In the second stage of VQ-VAE training, the encoder and codebook are frozen and a new, deeper, decoder is trained. This second stage of training has multiple purposes. First, a larger decoder improves reconstruction quality. Second, augmented structure tokens from ESM3 are added to enable learning pAE and pLDDT heads. Third, we add sequence conditioning and train with all-atom geometric losses to be able to decode all-atom protein structures. Fourth, we extend the context length of the decoder to be able to decode multimers and larger single chain proteins.
rom the PDB. Sequence conditioning was added to the decoder via learned embeddings which are summed with structure token embeddings at the input to the decoder stack.
The structure token decoder was trained in three stages: $2 \mathrm{~A}$, 2B, 2C detailed in Table S2. The purpose of stage 2A is to efficiently learn decoding of all-atom structures. Enhanced training efficiency is achieved by keeping a short context length and omitting the pAE and pLDDT losses, which are both memory-consuming and can be in competition with strong reconstruction quality. In stage $2 \mathrm{~B}$, we add the pAE and pLDDT losses. These structure confidence heads cannot be well-calibrated unless structure tokens are augmented such that ESM3-predicted structure tokens are within the training distribution. To this end, for stages $2 \mathrm{~B}$ and $2 \mathrm{C}$ we replace ground truth structure tokens with ESM3-predicted structure tokens $50 \%$ of the time. In stage $2 \mathrm{C}$, we extend context length to 2048 and upsample experimental structures relative to predicted structures.
All-atom Distance Loss: We generalize the Backbone Distance Loss to all atoms by computing a pairwise $L{2}$ distance matrix for all 14 atoms in the atom14 representation of each residue. This results in $D{\text {pred }}, D \in \mathbb{R}^{14 L \times 14 L}$. The rest of the computation follows as before: $\left(D_{\text {pred }}-D\right)^{2}$, clamping to $(5 \AA)^{2}$, and taking the mean, while masking invalid pairs (where any atom14 representations are "empty").
All-atom Direction Loss: We extend the Backbone Direction Loss to all heavy atoms:
(a) Compute a pairwise distance matrix per residue from the 3D coordinates of each atom in atom14 representation, resulting in $\mathbb{R}^{L \times 14 \times 14}$.
(b) Mark atoms less than $2 \AA$ apart (excluding self) as covalent bonds.
ng determined by the atom 14 representation.
(d) For each selected atom, compute a normal (zaxis) vector to the plane spanned by its two covalent bonds, resulting in three vectors per selected atom.
(e) Randomly subsample to 10,000 vectors per protein if the number exceeds 10,000 , ensuring the same vectors are sampled in both predicted and ground truth structures.
(f) Compute all-to-all pairwise dot products, forming $D{\text {pred }}, D \in \mathbb{R}^{n \times n}$. Compute $\left(D{\text {pred }}-D\right)^{2}$, clamp the max to 20 , and take the mean.
\section*{Computing Loss:}
(a) Compute the pairwise distances between residues in both the predicted and ground truth structures, resulting in distance matrices $D_{\text {pred }}$ and $D \in \mathbb{R}^{L \times L}$.
(b) Calculate the differences $\left(D_{\text {pred }}-D\right)$.
(c) Bin these differences into 64 bins, generating classification targets for the logits.
(d) Compute the loss using cross-entropy between these targets and the logits.
Computing pAE: Multiply probabilities by bin centers and sum to obtain the expected positional error per residue pair, with values $\in[0.25,31.75]$.
Computing pTM: Additionally, the pairwise logits are used to compute the pTM (Predicted Template Modeling) score, as follows:
(a) Compute $f_{d}$ for sequence length $L$ as:
$$ \begin{aligned} d_{0} & =1.24 \cdot(\max (L, 19)-15)^{\frac{1}{3}}-1.8 \
\text { bins }}{d_{0}}\right)^{2}} \end{aligned} $$
(b) Compute $\mathrm{pTM}$ using previously computed probabilities $p$ :
$$ \mathrm{pTM}=\max {i}\left[\frac{1}{L} \sum{j}\left(\sum{\text {bin }}[p]{i, j, \text { bin }}\left[f{d}\right]{\text {bin }}\right)\right] $$
\section*{A.1.7.4. EVALUATION}
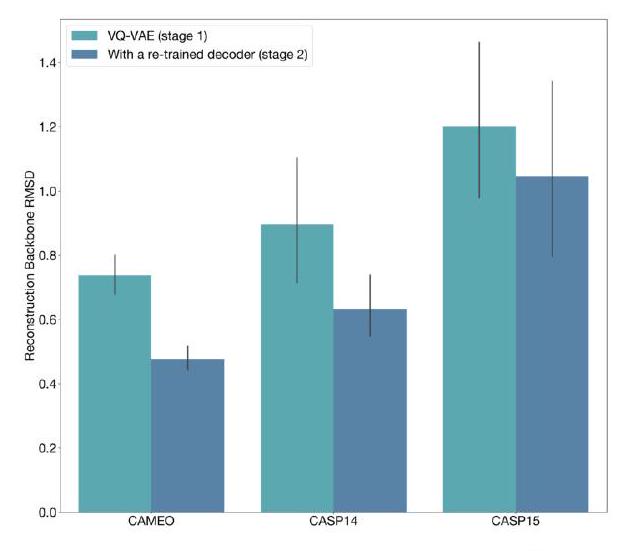
We evaluate the reconstruction quality of the structure tokenizer after stage 1 and stage 2 of training using a set of CAMEO, CASP14, and CASP15 proteins taken after the training cutoff date (Fig. S3). Both decoders consistently reach RMSD $<1 \AA$, LDDT-CA $>0.98$. The retraining of the structure token decoder results in substantial improvements in reconstruction quality across all test sets. The stage 2 decoder, trained with an all-atom reconstruction loss and a sequence input, achieves strong all-atom reconstruction as well (Fig. S3C). We also visualize a random sample of backbone reconstructions on the CAMEO test set (Fig. S4A). Looking at the proteins with worse reconstruction quality, we find that long regions with few tertiary contacts, disordered regions, and unresolved coordinates
\begin{tabular}{lllllll} \hline Stage & Steps & \begin{tabular}{l} All-atom \ geometric \ losses \end{tabular} & \begin{tabular}{l} pAE \ pLDDT \ losses \end{tabular} & \begin{tabular}{l} and \ with ESM3- \ predicted \ tokens \end{tabular} & \begin{tabular}{l} Data mixture \ length \end{tabular} & \ \hline 2A & $90 \mathrm{k}$ & $\checkmark$ & $X$ & $X$ & 512 & \begin{tabular}{l} Roughly uniform sampling of pre- \ dicted and experimental structures \end{tabular} \ 2B & $20 \mathrm{k}$ & $\checkmark$ & $\checkmark$ & $\checkmark$ & 512 & \begin{tabular}{l} Roughly uniform sampling of pre- \ dicted and experimental structures \end{tabular} \ 2C & $30 \mathrm{k}$ & $\checkmark$ & $\checkmark$ & & 2048 & \begin{tabular}{l} Upsampling experimental structures \end{tabular} \ \hline \end{tabular}
structure token decoder.
can lead to inaccurate global orientation of structural elements, while local structure reconstruction remains largely error-free (Fig. S4B). This behavior can be explained by the fact that the tokenizer relies on tertiary contacts to resolve the global orientation of a residue.
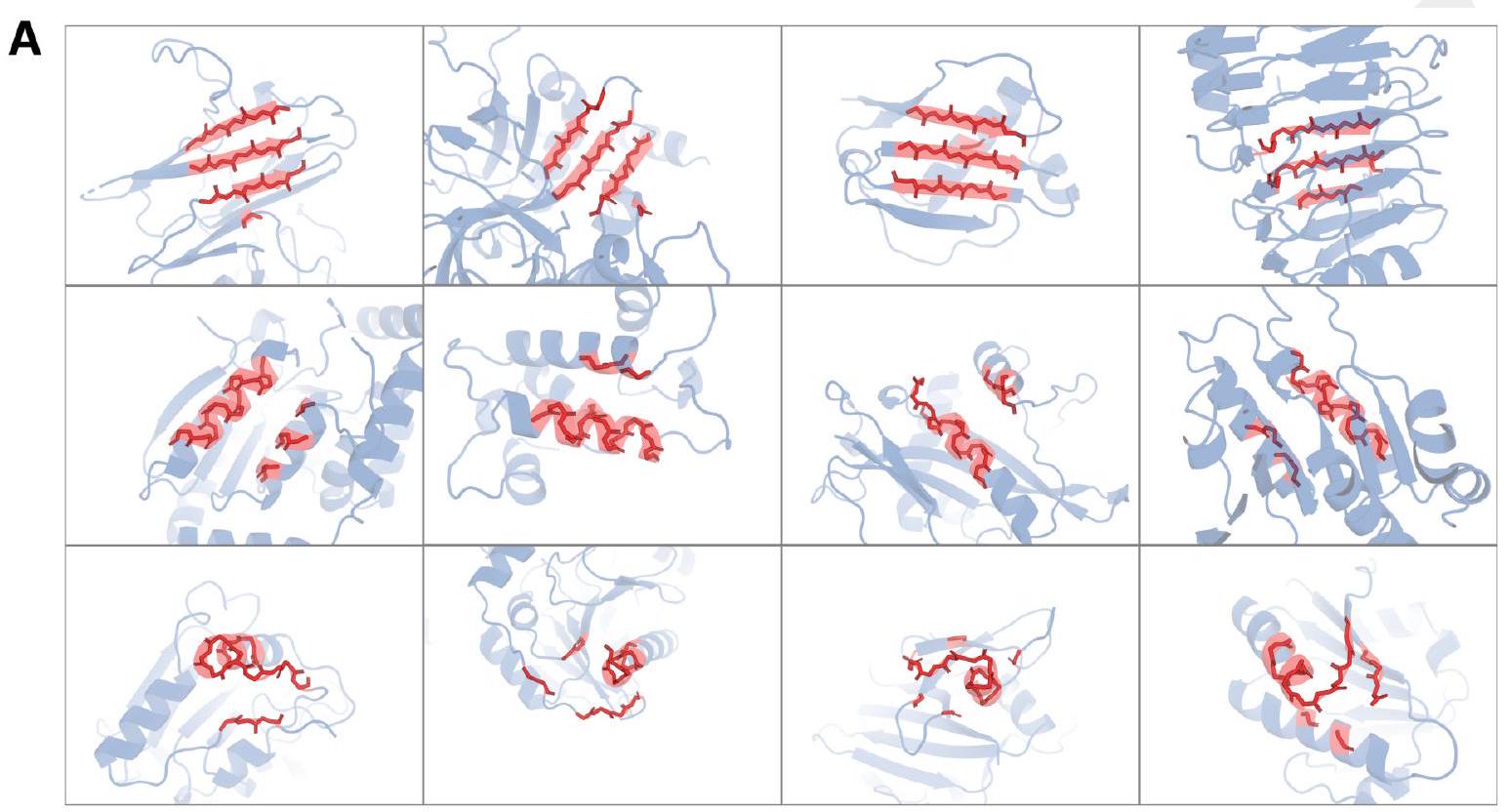
We also investigate the vocabulary learned by the structure tokenizer by visualizing the local neighborhoods which map to the same learned structure token. We find that many structure tokens encode semantically coherent sets of local neighborhoods (Fig. S5A). However, a number of tokens appear to represent multiple local neighborhoods (Fig. S5B). While the meaning of a single token may be ambiguous, the high-fidelity reconstruction quality from the decoder suggests that it is able to disambiguate given surrounding context in the full set of structure tokens.
Fig. S6 indicates that pLDDT and pTM are well-calibrated. We assess the calibration of the structure confidence heads on the CAMEO test set using structure tokens predicted by ESM3 7B. Most predictions for pLDDT lie along the diagonal, though there is a small bias towards more confident predictions. As pTM is a pessimistic estimator of the TMscore, we find that pTM is biased downwards. Anecdotally, we also find that pLDDT can be poorly calibrated for some generated sequences, particularly in alpha helical regions where it can be an overestimate.
\section*{A.1.8. Function Tokenization}
ESM3 processes annotations of functional characteristics of proteins through two tracks: function tokens, and residue annotations. Both support input conditioning and output heads for generation. Appendix A.1.5.1 outlines how tokens are processed into the network: we further describe the creation of the tokens themselves in this section.
\section*{A.1.8.1. FUNCTION TOKENS}
Ontology (GO) terms at each residue. At training time, function tokens are produced from each protein's InterPro annotations by a multi-step process illustrated in Fig. S7. At a high level:
For each residue, we gather free-text for each InterPro annotation via annotation term names, associated GO terms per annotation (via InterPro2GO mapping), and all ancestor GO terms. We parse the free-text into counts from a vocabulary of 68,103 keywords. The vocabulary is composed of unigram and bigrams extracted from the free-text of all valid InterPro annotations (and their associated GO/ancestor GO terms) in our training datasets.
The keywords are converted to a sparse TF-IDF vector per InterPro annotation. During training, we also produce a corrupted version by dropping keywords at the protein level (i.e. the same keywords have their counts set to 0 across all residues) at a $15 \%$ probability per keyword.
To create a vector per residue from the per annotation vectors, we max pool the TF-IDF vectors for the annotations per residue. During training, we further corrupt the "corrupted" version by dropping annotations at the protein level (i.e. the same annotations are removed from the max pool across all residues) at a $15 \%$ probability per annotation.
We then quantize each residue's vector (a highly sparse vector with float entries) into a discrete representation suitable for input to the language model as tokens by applying a fixed series of 8 locality sensitive hashes $(\mathrm{LSH})$, each with 8 hyperplanes.
The result is a sequence of 8 tokens each ranging in value from 0 to 255 per-residue. We reserve a special token
\section*{A}
oplefty=282&topleftx=232)
B
C
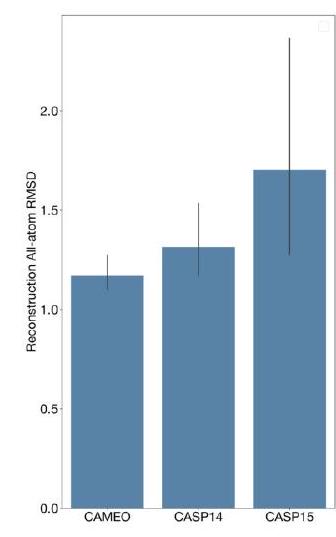
Figure S3. Structure tokenizer reconstruction quality. Reconstruction quality of the structure tokenizer after stage 1 and stage 2 of VQ-VAE decoder training evaluated on temporally held out CAMEO, CASP14, and CASP15. (A) Reconstruction LDDT-CA. (B) Reconstruction backbone RMSD. (C) All-atom reconstruction RMSD from the stage 2 decoder which additionally receives sequence input.
time, we can produce per residue vectors using the process described, or directly creating a TF-IDF vector with keywords.
During pre-training we use the corrupted versions of the function tokens at input, predicting the un-corrupted version function tokens at positions which have been masked. $90 \%$ of the time, the entire input is replaced with $<$ mask $>$. The other $10 \%$ of the time, we replace all 8 tokens of selected residue with a $<$ mask $>$, with the per-residue selection probability sampled from a cosine masking schedule per protein. The model has an output head which predicts each of the 8 function tokens in positions with $<$ mask $>$ as input, and is trained with a categorical cross entropy loss
Function tokenization offers several key advantages as compared to simpler approaches for example using a dedicated InterPro tag vocabulary. Encoding functional annotations with a generic functional keyword vocabulary enables flexible prompting of the model at test time, by combinations of keywords that were not encountered during training time. This enhances the programmability of ESM3 in designing novel proteins with not previously observed functional characteristics.
input/output space from all possible InterPro combinations which would naively be represented by $35 \mathrm{k}$ bits, to a reduced space of 8 tokens $\times 8$ bits $/$ token $=64$ bits. This also affords significant memory saving during pre-training by eliminating the need to perform multi-class multi-label binary classification.
\section*{A.1.8.2. FUNCTION PREdiCTION}
ESM3 is trained to predict all 8 function tokens, each spanning 256 possible values. To extract interpretable predictions of protein function from ESM3 we decode the predicted function tokens into function keywords using a seperately trained function token decoder.
\section*{A.1.8.2.1. Function Token Decoder}
We train a 3-layer transformer model to learn the inverse map of the function tokenization process. The model takes as input the 8 function tokens representing the locality sensitive hash of function keywords. It outputs for each residue the binary-classification predictions predicting the presence of each function keyword, as well as predicting InterPro annotations from which the keywords originate. We find that unpacking the 8-bit LSH tokens into single-bit tokens improves training dynamics of the function token decoder. We train the function token decoder offline using combinations of InterPro tags from the UniRef annotated proteins. Since the function token vocabulary is fixed the decoder is applied identically across different ESM3 model sizes.
\section*{A.1.8.2.2. Evaluation}
To evaluate ESM3's performance in predicting protein function, we compute Average Precision, a standard measure of information retrieval, using the validation set of proteins from the UniRef and their associated InterProScan function annotations. We present results in Fig. S8.
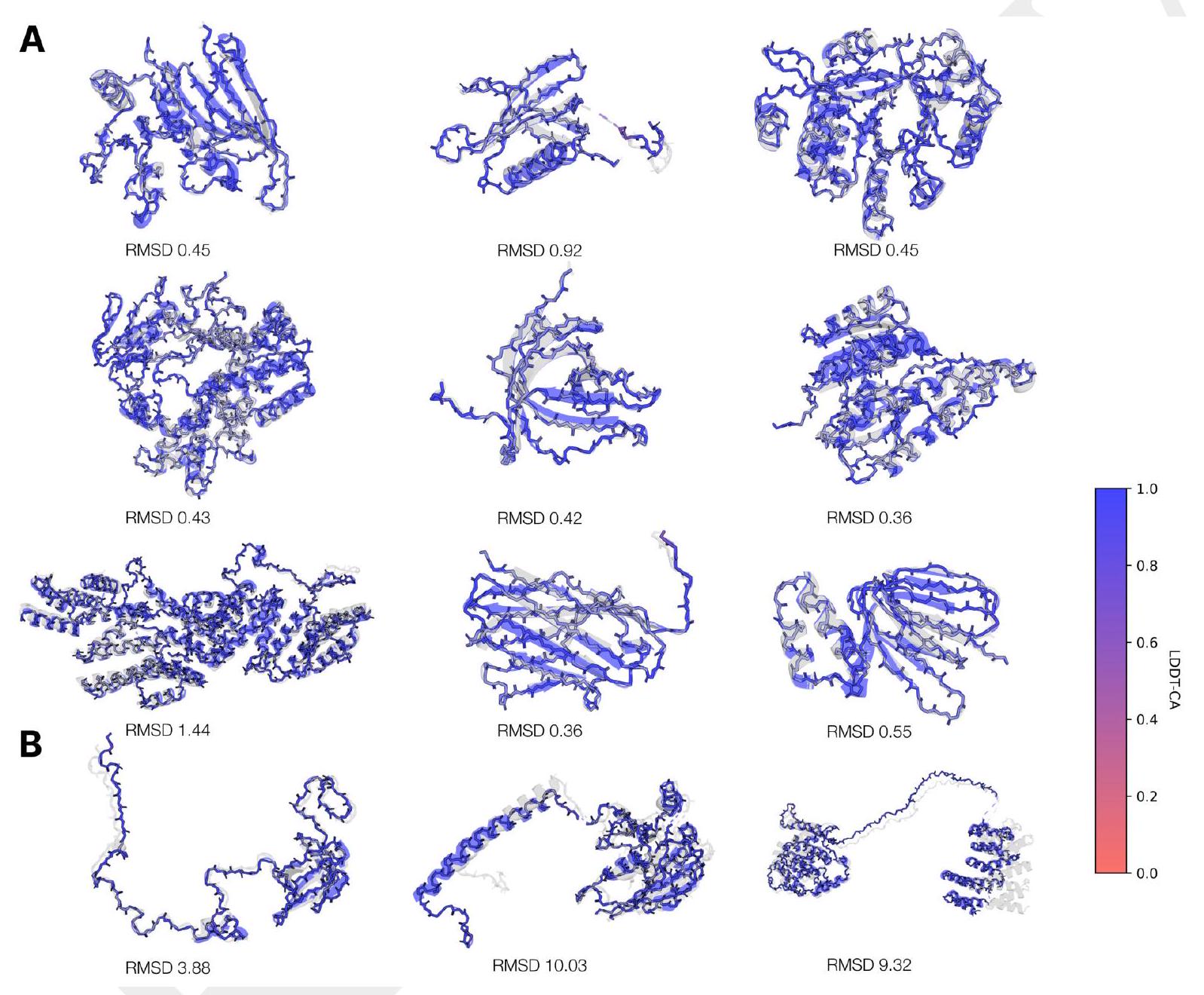
ctions from the structure tokenizer on the CAMEO test set. The vast majority of structures have near perfect backbone reconstruction (B) A selection of the worst reconstructions in CAMEO. Long stretches of disordered regions, a lack of tertiary contacts, and unresolved coordinates can lead to inaccurate global orientation of structural elements, while local structure reconstruction remains largely error-free.
B
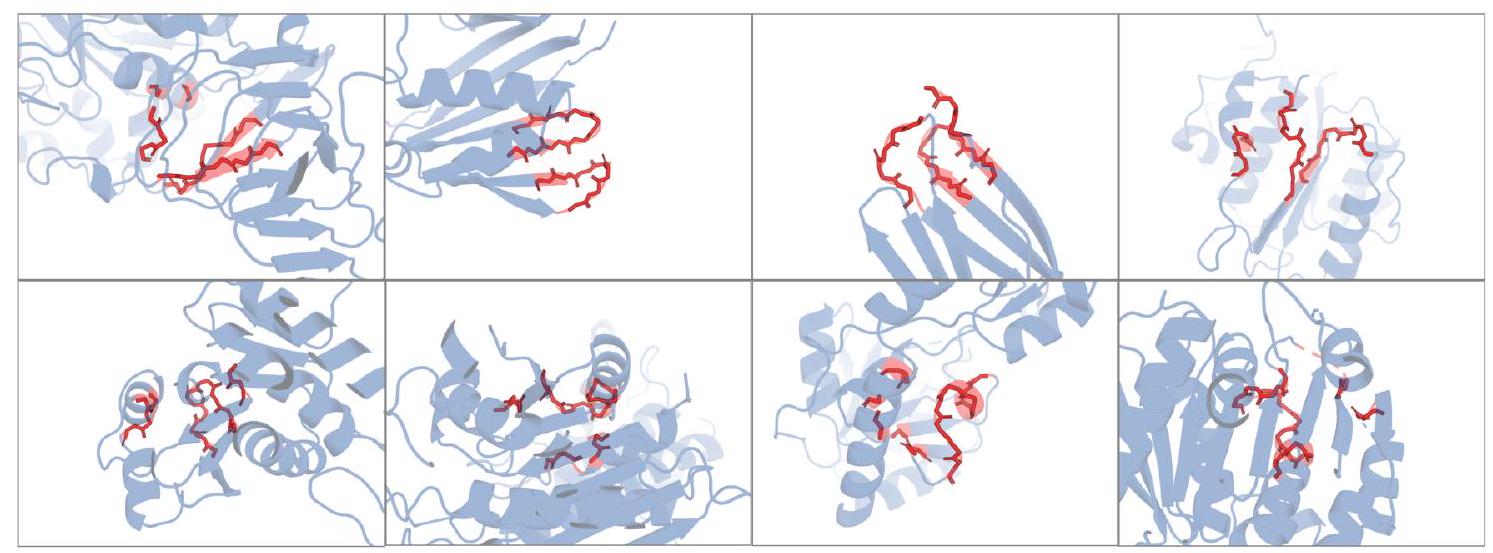
Figure S5. Visualization of local neighborhoods which map to the same learned structure token. The VQ-VAE encoder reasons over local structure neighborhoods (highlighted in red) which include the query residue and the 15 nearest neighbors in structure space. (A) Rows correspond to token indices 585,59 , and 3692 for top, middle, and bottom, respectively. Columns show different local structures mapping to the same token. (B) Some tokens represent multiple types of local neighborhoods. All local neighborhoods in B map to the same codebook index 3276. While the meaning of a single token may be ambiguous, the decoder is able to disambiguate given surrounding context in the full sequence of structure tokens.
Figure S6. pTM and pLDDT calibration. Calibration of the structure token decoder pLDDT and pTM (using ESM3 7B as the structure token prediction model) on the CAMEO test set.
nsitive hash to produce 8 tokens each containing 8 bits.
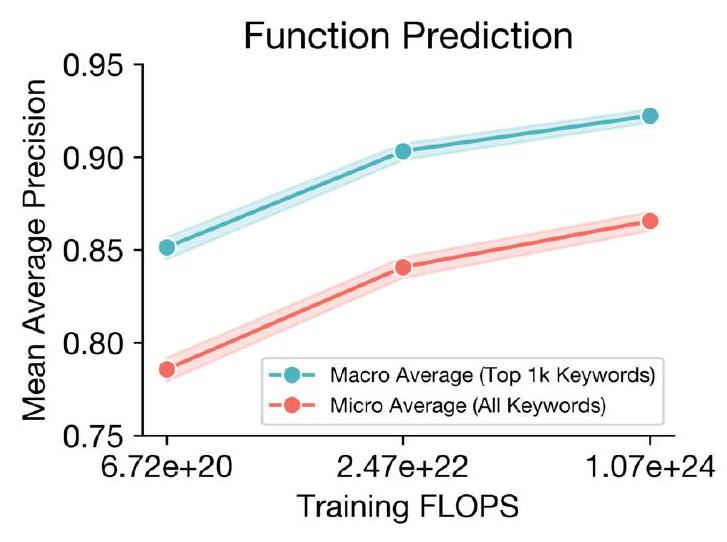
Figure S8. Function prediction benchmarking results. Mean Average Precision (mAP) for function keyword prediction. Predictions and labels are compared on a per-position basis to evaluate the model's ability to localize site-specific functional attributes by keywords such as "active site". We report mAP for the full keyword set (red) with a "micro" average because many keywords have few or no labels in the validation set. To report a "macro" average mAP we compute mAP for each of the top 1,000 most prevalent keywords in our evaluation set (discarding uninformative keywords such as "the") and report a uniform average (blue). $95 \%$ confidence intervals are shown by shading.
\section*{A.1.8.3. Residue Annotations Track}
Residue annotations label a protein's sites of functional residues with a vocabulary of 1474 multi-hot labels emitted by InterProScan. To gather this data, we run InterProScan with databases (SFLD, CDD, PIR) on all cluster members in our UniRef and Mgnify datasets (seq-id 90 clustered). We take all unique residue annotation descriptions that occur in more than $1 \mathrm{k}$ proteins across all of UniRef90 and MGnify 90 , and deduplicate labels by punctuation and case insensitivity. We join these annotations into our UniRef, MGnify, AFDB, and ESMAtlas datasets for training.
e permutation invariance of the sum retains that the labels are represented to an unordered set as a model. The per-position embedding sums are then added onto the per-position sequence embedding before input into the first transformer block. Positions with no residue annotations are represented by a
\section*{A.1.9. Other Tracks}
\section*{A.1.9.1. Confidence TRackS}
As mentioned in Appendix A.1.5.1, ESM3 has two additional tasks that are only used during pre-training, and only used as input (we do not have output heads predicting these values). The first is a per-residue pLDDT: for ground truth PDB structures, these values are all 1; for AlphaFoldDB/ESMFold structures, we use the provided pLDDT. We also provide an averaged pLDDT across all the residues when structure is provided (1 otherwise), with the average calculated before any tokens are masked.
This information allows the model to distinguish between gold-standard structures and computationally predicted ones; at inference time, we set these to 1 throughout, with the goal of producing structures better than the computational predictions used to pre-train the model. The embedding itself is straightforward, with the pLDDT values first having a radial basis function, followed by a Linear layer applied to them:
Algori
------------------------------
- The per-position embedding sums are added onto the per-position sequence embedding before input into the first transformer block.
- Positions with no residue annotations are represented by a <pad> token which has an embedding fixed to zeros.
- The residue annotations track has an output head which outputs a set of binary classification logits predicting for each position the presence or absence of each residue annotation in the vocabulary.
- A masking procedure is applied to partially/fully mask residue annotation labels.
- The output head is trained with a binary cross-entropy loss function to reconstruct the full residue annotation.
- In pre-training, with $90 \%$ probability all residue annotations are masked, and otherwise we independently sample positions to mask with a square root schedule.
- The head is trained to predict the presence of any residue annotation label that was masked.
- ESM3 has two additional tasks that are only used during pre-training, and only used as input.
- The first is a per-residue pLDDT.
- For ground truth PDB structures, these values are all 1.
- For AlphaFoldDB/ESMFold structures, we use the provided pLDDT.
- We also provide an averaged pLDDT across all the residues when structure is provided (1 otherwise), with the average calculated before any tokens are masked.
- This information allows the model to distinguish between gold-standard structures and computationally predicted ones.
- At inference time, we set these to 1 throughout, with the goal of producing structures better than the computational predictions used to pre-train the model.
- The embedding itself is straightforward, with the pLDDT values first having a radial basis function, followed by a Linear layer applied to them.
User:
==============================
thm 12 rbf
Input: $x \in \mathbb{R} \cdots \times L, a \in \mathbb{R}, b \in \mathbb{R}, n \in \mathbb{Z}^{+}$
$: \Delta=\frac{b-a}{n-1} \quad \quad \triangle \mathbb{R}$
$c=[a, a+\Delta, a+2 \Delta, \ldots, a+(n-2) \Delta, b] \quad \triangleright \mathbb{R}^{n}$
$\sigma=\frac{b-a}{n} \quad \triangle \mathbb{R}$
$[z]_{\ldots, i, j}^{n}=\frac{1}{\sigma}\left([x]_{\ldots, i}-[c]_{j}\right) \quad \triangle \mathbb{R}^{\cdots} \times L \times n$
return $\exp \left(-z^{2}\right) \quad \triangleright \mathbb{R} \cdots \times L \times n$
Algorithm 13 plddt_embed
Input: $x_{\text {plddt }} \in[0,1]^{L}, x_{\text {argplddt }} \in[0,1]$
$\operatorname{rbf}_{\text {plddt }}=\operatorname{rb} f\left(x_{\text {plddt }}, 0.0,1.0,16\right) \quad \triangle \mathbb{R}^{L \times 16}$
$\mathrm{rbf}_{\text {avgplddt }}=\operatorname{rb} f\left(x_{\text {avgplddt }}, 0.0,1.0,16\right) \quad \triangle \mathbb{R}^{16}$
$z_{\text {avgplddt }}=\operatorname{Linear}(\mathrm{rbf}$ avgplddt $) \quad \triangle \mathbb{R}^{d}$
$z_{\text {plddt }}=$ Linear(rbf plddt $) \quad \triangle \mathbb{R}^{L \times d}$
$\left[z_{\text {plddt }}\right]_{i,:}=\left[z_{\text {plddt }}\right]_{i,:}+z_{\text {avgplddt }} \quad \triangleright \mathbb{R}^{L \times d}$
return $z_{\text {plddt }}$
\section*{A.1.9.2. TAXONOMY TRACK}
This low-rank embedding bag saves memory as compared to using full-dimension embeddings. This single embedding is then repeated across the length of the sequence and summed into the positional embeddings with all the other tracks. The linear projection is zero-initialized at the start of this stage of training to preserve model behavior, enabling continuation of pre-training with no degradation in performance.
In pre-training we apply random corruption to the taxonomic lineages and train ESM3 to reconstruct the full lineage by predicting dropped terms with a shallow MLP head trained on the final layer's representations. To corrupt the taxonomic lineage, we either drop all terms (probability 25\%) or drop a set of the most specific terms of the lineage of size chosen uniformly at random from 1 to the length of the lineage (probability $25 \%$ ). We also independently drop any taxonomic term with probability $10 \%$. The output head outputs binary classification logits over the full set of 40,000 taxonomic lineage terms, and is trained to predict the missing terms via a binary-cross entropy loss.
\section*{A.1.10. ESM3 Inference}
Since ESM3 is a bidirectional transformer capable of representing arbitrary factorizations of the joint probability in any order or combination of tracks, we have significant flexibility during inference: We can generate sequence, structure, or function conditioned on any or no combination of other tracks. We also have a choice of how much compute to apply during generation.
in the length of the protein and is extremely efficient. Iterative decoding, on the other hand, samples tokens one position at a time, conditioning subsequent predictions on those already sampled. The runtime for iterative decoding, comparable to slower algorithms such as ESMFold and AlphaFold, is $O\left(L^{3}\right)$ in the length of the protein.
Additionally, the number of decoding steps can be chosen at runtime. Argmax decoding is equivalent to decoding in one step, while iterative decoding is equivalent to decoding in $L$ steps. It is possible to select any number of decoding steps between these two extremes to find an optimal tradeoff between computation and accuracy for a particular use case. See Appendix A.3.4 for a case study in the case of structure prediction, in which the generation track is the structure tokens track.
When using iterative decoding, ESM3 further allows flexibility in choosing the next position to decode. We choose the position based off of the logits output of ESM3, and for the results of this paper utilize two strategies: entropy decoding, which chooses the position with the lowest entropy after softmax, or max logit decoding, which chooses the position with the maximum logit. To generate $k$ tokens in one pass, we rank by either entropy or max logit and take the top $k$ positions.
In the following algorithm, assume a single forward pass of ESM3 is a function $f$ of a prompt $x$, and that we can access the logits of a specific token track through a subscript; e.g. sequence logits would be $f_{\text {sequence }}(x) \in \mathbb{R}^{L \times 32}$. Furthermore, denote $\pi(\cdot ; z)$ as the probability distribution induced by the logits $z$, including an implicit softmax, and $T \in \mathbb{R}^{L}$ a temperature schedule.
Algorithm 14 generate from track
Input: $x_{\text {prompt }}, n_{\text {decode }} \in\{1 . . L\}, T \in \mathbb{R}^{n_{\text {decode }}}$
: $k=L / n_{\text {decode }} \quad \triangleright \#$ steps to decode
------------------------------
1. $z_{0}=\operatorname{argmax}_{z} \pi(z ; f_{\text {sequence }}(x))$
2. $x_{0}=z_{0}$
3. $p_{0}=T_{0}$
4. $\text { for } i=1 \text { to } n_{\text {decode }}-1$
5. $\quad$ $z_{i}=\operatorname{argmax}_{z} \pi(z ; f_{\text {sequence }}(x \mid x_{i-1}))$
6. $\quad$ $x_{i}=z_{i}$
7. $\quad$ $p_{i}=T_{i}$
8. $\text { return } x_{n_{\text {decode }}}$
In the above algorithm, $x{i}$ is the $i$ th token generated, $z{i}$ is the logit vector of the $i$ th token, and $p{i}$ is the temperature used to generate the $i$ th token. The prompt $x$ is updated to $x{i-1}$ for the next token generation.
In the case of entropy decoding, $T{i}$ is set to $1 / \operatorname{logitmax}(f{\text {sequence }}(x \mid x{i-1}))$, where $\operatorname{logitmax}(\cdot)$ is the maximum logit of the input. In the case of max logit decoding, $T{i}$ is set to $1 / \max \pi(z ; f{\text {sequence }}(x \mid x{i-1}))$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
In the case of $n{\text {decode }}=L$, the above algorithm is equivalent to argmax decoding. In the case of $n{\text {decode }}=1$, the above algorithm is equivalent to iterative decoding with $T=1$.
at each step for $s \in\left{1 . . n{\text {decode }}\right}$ do $z{\text {logits }}=$ esm3forward $\left(x{\text {prompt }}\right) \triangleright z \in \mathbb{R}^{L \times c{\text {track }}}$ $\left{p{1}, \ldots, p{k}\right}=$ CHOosePositions $(z)$ for $i \in\left{p{1}, \ldots, p{k}\right}$ in parallel do $x{i} \sim \pi\left(x ; z{i} / T{s}\right) \quad \triangle$ Sample $i$ with temp $T{s}$ $x{\text {prompt }}=\left{x{\text {prompt }}, x{i}\right} \quad \triangleright$ Update prompt end for end for ```